elibaum.com
[paper] orq: complex analytics on private data
16 Sep 2025
Our paper, ORQ: Complex Analytics on Private Data with Strong Security Guarantees, has been accepted to SOSP 2025! This is the first big paper of my PhD, and the culmination of nearly two years of work for me and my wonderful coauthors.
Oblivious algorithms must always preserve worst-case sizes. This poses a challenge for efficiently implementing many common analytics. A simple example is an oblivious filter: given \(n\) input elements, it must return \(n\) output elements, since a smaller output would leak the number of matches to the filter. Here, it is easy to just append a secret-shared “valid” bit to each record denoting whether it should be included in the output or not.
Joins are more complex: an arbitrary join between two tables of size \(n\) could have output size \(n^2\) (the Cartesian product). Thus an oblivious join must preserve this worst-case size and output \(n^2\) records. At first glance, this may not seem terrible, but the real issue is that multiple successive joins each add a factor of \(n\) to the output size! Thus, performing \(k\) joins in a row has an inherent worst-case output of \(O(n^{k+1})\).
We make a number of contributions on the efficient implementation of multiparty computation, but our main insight is that nearly all real-world queries perform group-by aggregations immediately after joins. This allows for a critical optimization, because a table of size \(n\) has at most \(n\) groups:1
Table A(n) = {...}
Table B(n) = {...}
Table C(n) = {...}
# upper bound on size: n^2
T1 = A.Join(B, ...)
# upper bound: n
T2 = T1.Aggregate(B.groupKey, function, ...)
# upper bound: n^2 (but would have been n^3 before)
T3 = T2.Join(C, ...)
# upper bound: n
T4 = T3.Aggregate(C.groupKey, function, ...)
Is it possible to combine these two steps, and somehow avoid the quadratic intermediate? Yes, it is! We can “fuse” the control flow of join and aggregation, perform some rewritings under relational algebra, and evaluate arbitrarily complex queries in \(O(n \log n)\) time!2
We also contribute efficient, parallelized implementations of oblivious quicksort and radixsort, which are pretty cool in their own right. Historically, many MPC papers have used bitonic sort, which runs in \(O(n \log^2 n)\) time.
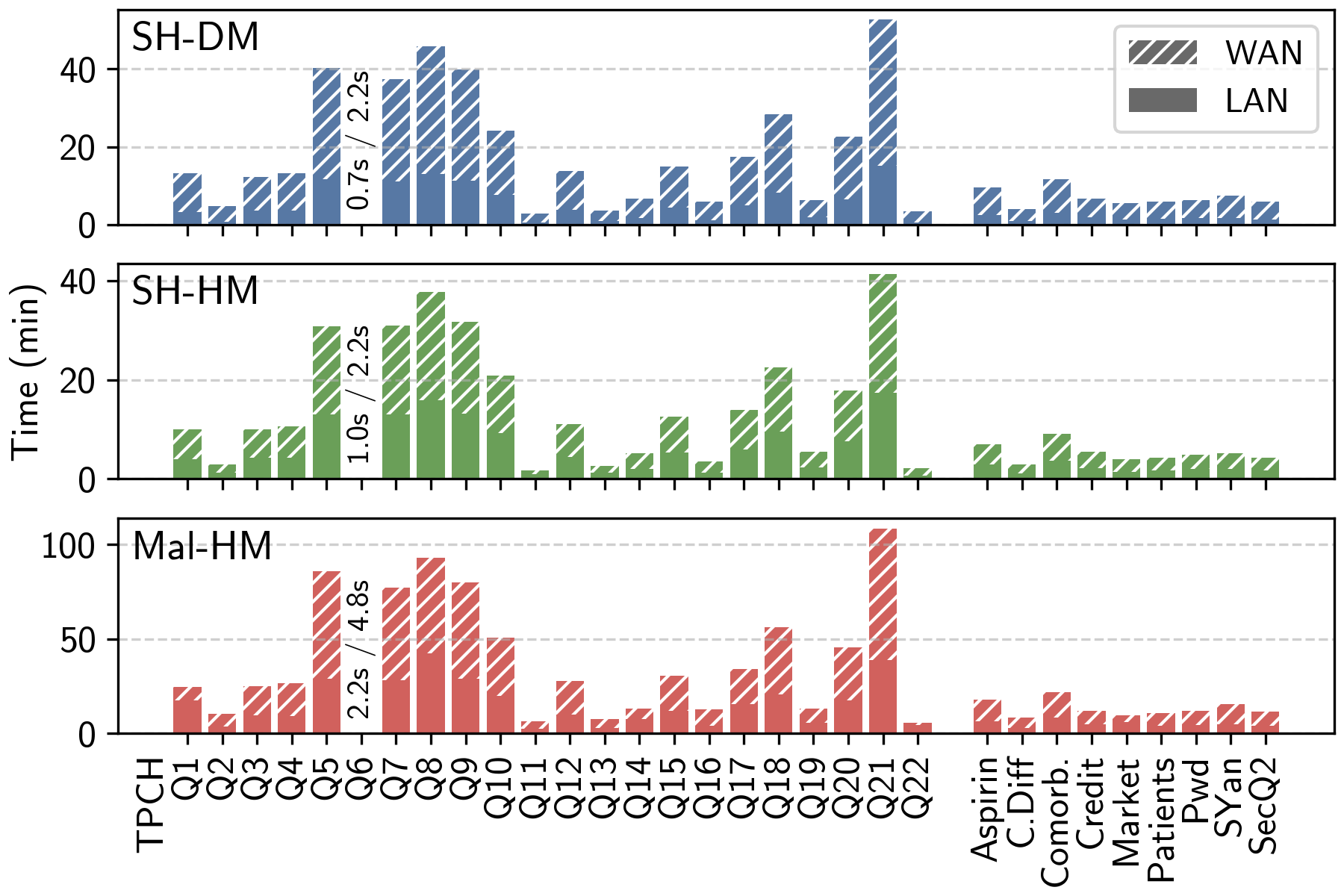
Performance highlight: we evaluate the entire TPC-H relational benchmark at Scale Factor 1, requiring, on average, only a few minutes per query in LAN. Some of these queries have up to seven joins. To our knowledge, this is the first time anyone has evaluated the full benchmark under MPC.
We want ORQ to be a easy-to-use framework for experimentation with secure analytics. Give it a try, and open an issue or pull request on Github if you have any questions or suggestions!