elibaum.com

a bad pseudorandom function

15 Mar 2024

Assume \(G(s)\) is a secure pseudorandom generator. Then (according to Leo) \(F_k(x)=G(k\oplus x)\) is not a secure PRF. Why?

We’re going to use, as a counterexample, the one-bit-expanding Blum-Micali PRG:

\[G(s) = g^s \bmod p\ ||\ \beta(s)\]

for some prime \(p\), generator \(g\), and where \(\beta(s)\) returns the MSB of \(s\).¹

Warm up

The intuition here is that XORing the key and seed imparts some unacceptable structure on the PRF. This is easier to see if you consider addition, instead; \(F’_k(x)=G(k+x)\).

\[\begin{align} F'_k(x) &= G(k+x) \\ &=g^{k+x} \bmod p\ ||\ \beta(k + x)\\ &=g^k g^x \bmod p\ ||\ \beta(k + x)\\ \end{align}\]

\(\beta(k+x)\) is not necessarily known, but if \(x\) is small, then \(\beta(k + x)\approx\beta(k)\) w.h.p. Let \((z_L, z_R) = F’_k(0)\). Then,

\[F'_k(x) \approx g^x \cdot z_L || z_R\]

So, given the evaluation of the PRF at zero (or really any fixed point), we can extract the value of the PRF for an arbitrary input, merely by multiplying by \(g^x\) (and maybe flipping the last bit, if \(x\) is large). Not good!

Extending to XOR

The same idea works with XOR, but it’s a bit more involved on the LHS. The right side is actually easy: \(\beta(k\oplus x)=\beta(k)\oplus\beta(x)\).

As above, let \( (z_L, z_R) = F_k(0) = G(k\oplus 0) = g^k \bmod p\ ||\ \beta(k) \). To handle the XOR, we need to consider the bitwise representation of the PRG: let \(x_i\in\{0,1\}\) be the \(i\)-th bit of \(x\). Then, \(x=\sum_i 2^i x_i\) and \(g^x=\prod_i g^{2^i x_i}\). We can expand the PRG construction as follows:

\[\begin{align*} g^{k\oplus x}&=g^{\sum_i(2^i[k\oplus x]_i)}\\ &=g^{\sum_i\left(2^i[k_i+x_i-2k_ix_i]\right)}&\text{algebraic representation of }\oplus\\ &=g^{\sum_i2^ik_i+\sum_i2^ix_i-2\sum_i2^ik_ix_i}\\ &=g^{k+x-2\sum_i2^ik_ix_i}\\ &=g^kg^xg^{-2\sum_i2^ik_ix_i} \end{align*}\]

Define \(h=g^{-2}\):

\[\begin{align*} F(k\oplus x)&=g^k g^x \prod_i h^{2^ik_ix_i}\bmod p\ ||\ \beta(k\oplus x)\\ &=z_L\left(g^x\prod_i h^{2^ik_ix_i}\right)\bmod p\ ||\ z_R \oplus\beta(x) \end{align*}\]

The adversary (trying to guess \(F_k(x)\)) already knows \(z_L, z_R, \beta(x),g^x\). The inner product is difficult so compute… but it is equivalent to \(h^{k\wedge x}\). So, we have an interesting attack: we only have to guess those bits of the key for which \(x\) also has a set bit; equivalently, given \(F_k(0)\), we can determine the evaluation of the PRF for low-weight \(x\).

Does this actually work?

Implementing the attack

Yes! Some quick python code implements this attack, with the simulated success probability closely tracking the math. The meat of the attack looks like this:

# A random x to look at
x = random.randint(1, 2 ** MAX_EXP)
# The rand() below is a random key. `guess` is our guess for k & x 
guess = rand() & x

# Left side of the PRG
newL = (zL * pow(gen, x - 2 * guess, P)) % P
# Right side
newR = zR ^ beta(x)

maybe_prf = (newL << 1 | newR)

####
## secret section
true_value = bad_prf(k, x)
is_correct = true_value == maybe_prf
#####

hw = x.bit_count()

We run the above in a loop, monitoring success probability binned by hamming weight. I used \(p=4294967087\) but of course, in reality, you would want a much larger group (the results hold for longer primes, but simulation takes significantly longer).

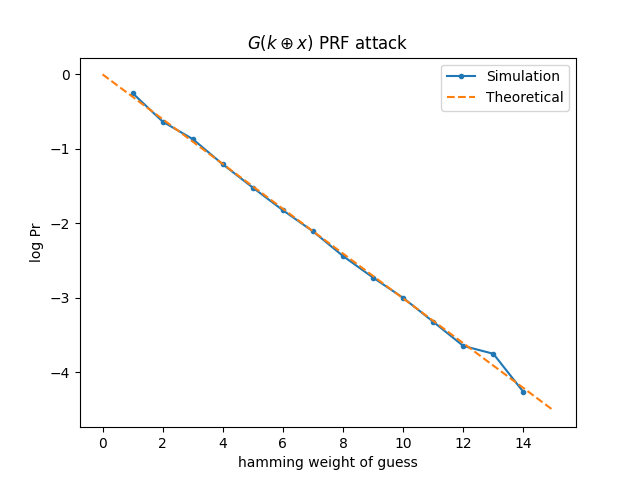
Vertical axis is \(\log_{10}\Pr\), so -1 is 10%, etc. For hamming weight of 1 (i.e., \(x\) is a power of two), we succeed with probability \(1/2\). The dashed “theoretical” line is \(\Pr[w]=2^{-w}\). The results above were generated with 1M iterations of the attack.

The full python script is available here.

1. Technically, whether \(s>p/2\). ↩